Arxiv
Code
*equal contribution
Code will be released soon.
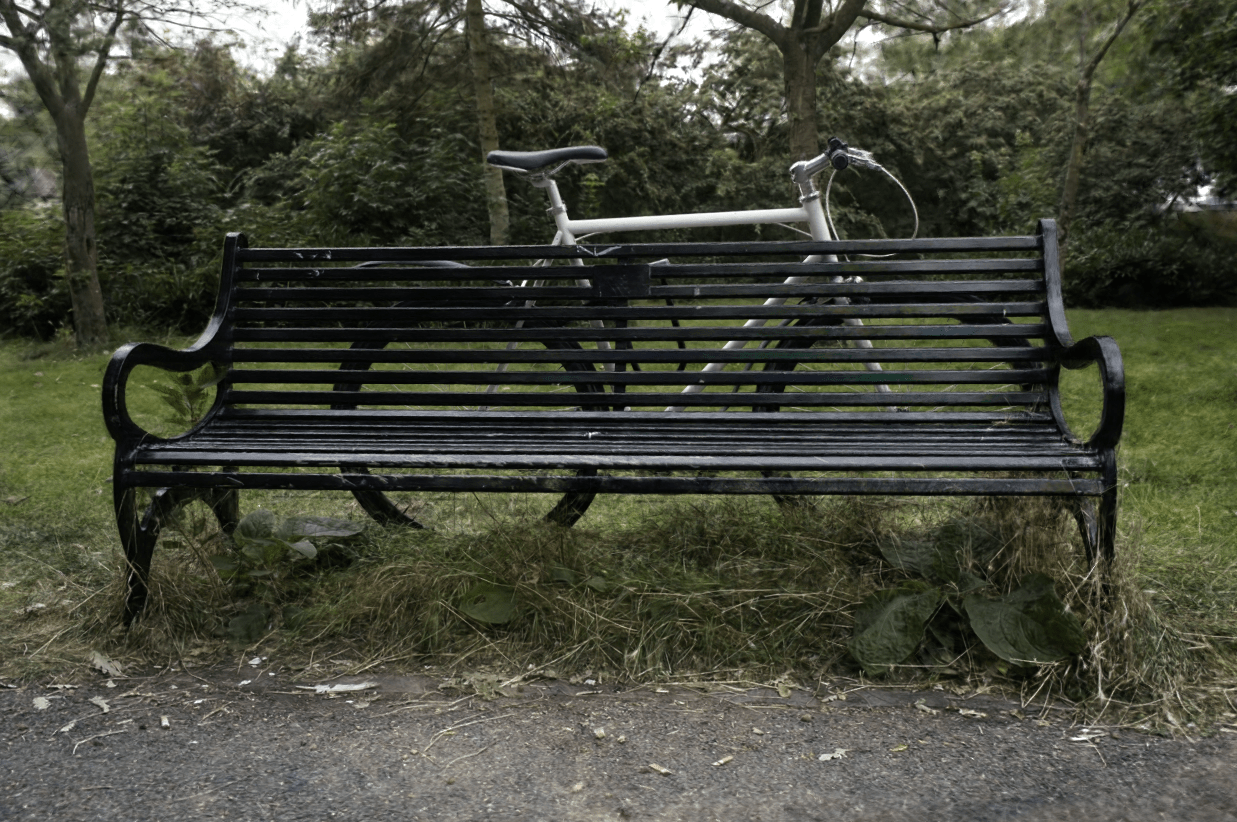
Triangle Splatting achieves high-quality novel view synthesis and fast rendering by representing scenes with triangles. In contrast, the inherent softness of Gaussian primitives often leads to blurring and a loss of fine details, for example, beneath the bench or at the room’s door, whereas Triangle Splatting preserves sharp edges and accurately captures fine details.
The field of computer graphics was revolutionized by models such as Neural Radiance Fields and 3D Gaussian Splatting, displacing triangles as the dominant representation for photogrammetry. In this paper, we argue for a triangle come back.. We develop a differentiable renderer that directly optimizes triangles via end-to-end gradients. We achieve this by rendering each triangle as differentiable splats, combining the efficiency of triangles with the adaptive density of representations based on independent primitives. Compared to popular 2D and 3D Gaussian Splatting methods, our approach achieves higher visual fidelity, faster convergence, and increased rendering throughput. On the Mip-NeRF360 dataset, our method outperforms concurrent non-volumetric primitives in visual fidelity and achieves higher perceptual quality than the state-of-the-art Zip-NeRF on indoor scenes.
Triangles are simple, compatible with standard graphics stacks and GPU hardware, and highly efficient: for the Garden scene, we achieve over 2,400 FPS at 1280×720 resolution using an off-the-shelf mesh renderer. These results highlight the efficiency and effectiveness of triangle-based representations for high-quality novel view synthesis. Triangles bring us closer to mesh-based optimization by combining classical computer graphics with modern differentiable rendering frameworks.
Our rendering pipeline uses 3D triangles as primitives, each defined by three learnable 3D vertices, color, opacity, and a smoothness parameter \( \sigma \). The triangles are projected onto the image plane using a standard pinhole camera model with known intrinsics and extrinsics.
Instead of binary masks, we introduce a smooth window function that softly modulates the triangle's influence across pixels. This function is derived from the 2D signed distance field (SDF) of the triangle, which measures the distance from a pixel \( \mathbf{p} \) to the triangle’s edges.
The signed distance field \( \phi(\mathbf{p}) \) is defined as the maximum of three half-plane distances:
\( \phi(\mathbf{p}) = \max\left( L_1(\mathbf{p}),\; L_2(\mathbf{p}),\; L_3(\mathbf{p}) \right) \)
where each half-space function is defined as:
\( L_i(\mathbf{p}) = \mathbf{n}_i \cdot \mathbf{p} + d_i \)
with \( \mathbf{n}_i \) denoting the outward-facing unit normal of the \( i \)-th edge, and \( d_i \) its signed offset from the origin.
The final window function is:
\( I(\mathbf{p}) = \text{ReLU}\left( \frac{\phi(\mathbf{p})}{\phi(\mathbf{s})} \right)^\sigma \)
where \( \mathbf{s} \) is the triangle’s incenter, i.e., the point where \( \phi \) is minimized. This function satisfies:
The figure above illustrates how the window function behaves in 1D and 2D. As \( \sigma \to 0 \), the function approximates a binary triangle mask. As \( \sigma \) increases, the transition becomes smoother, and in the limit \( \sigma \to \infty \), it becomes a delta function centered at \( \mathbf{s} \).
To render an image, we accumulate contributions from all projected triangles using alpha blending in front-to-back depth order. Since all steps are differentiable, we can optimize the triangle parameters using gradient-based learning.
Triangle Splatting produces sharper and more detailed images. Notably, it renders the flowers and the background with greater realism and captures finer details compared to 3DGS or 3DCS. (If the videos appear out of sync, please reload the page to ensure proper alignment.)
Triangle Splatting unifies differentiable scene optimization with traditional graphics pipelines. The triangle soup is compatible with any mesh-based
renderer, enabling seamless integration into traditional graphics pipelines.
In a game engine, we render at 2400+ FPS at 1280×720 resolution on an RTX4090.
The current visuals are rendered without shaders and were not specifically trained or optimized for game engine fidelity, which accounts for the limited visual quality.
Nevertheless, it demonstrates an important first step toward the direct integration of radiance fields into interactive 3D environments.
Future work could explore training strategies specifically tailored to maximize visual fidelity in mesh-based renderers, paving the way for seamless integration of reconstructed scenes into standard game engines for real-time applications such as AR/VR or interactive simulations.
The triangles are well aligned with the underlying geometry. All triangles share a consistent orientation and lie flat on the surface.
@article{Held2025Triangle,
title = {Triangle Splatting for Real-Time Radiance Field Rendering},
author = {Held, Jan and Vandeghen, Renaud and Deliege, Adrien and Hamdi, Abdullah and Cioppa, Anthony and Giancola, Silvio and Vedaldi, Andrea and Ghanem, Bernard and Tagliasacchi, Andrea and Van Droogenbroeck, Marc},
journal = {arXiv},
year = {2025},
}